\(T_{2}^*\) Ramsey (1-2 states)

This experiment provides a more accurate estimate of the qubit's resonance frequency between the first and second excited states, \(\omega_{q12}\), and an estimate of the coherence time of this transition.

Description

The qubit resonance frequency between the first and second excited states, \(\omega_{q12}\), determined using Pulsed qubit spectroscopy (1-2 states) tends to be slightly detuned from its actual value due to finite pulse duration, power broadening, environmental noise, and imperfect fitting of the Lorentzian function. While this serves as a good first guess for \(\omega_{q12}\), the Ramsey experiment uses the phase evolution of the qubit to obtain a much more precise value.

This experiment is very similar to \(T_{2}^*\) Ramsey; however, prior to the standard Ramsey pulse sequence, a \(\pi\)-pulse is applied to prepare the qubit in the first excited state \(|1\rangle\).

State preparation (\(R_{01}(\pi)\))

The sequence begins with a \(\pi\)-pulse at the fundamental frequency \(\omega_{q01}\). This flips the qubit from the ground state \(|0\rangle\) to the first excited state \(|1\rangle\), which serves as the "ground" state for the subsequent Ramsey sequence.

\(\frac{\pi}{2}\)-pulse (\(R_{12}\!\left(\frac{\pi}{2}\right)\))

A \(\frac{\pi}{2}\)-pulse resonant with the 1-2 transition is applied. This prepares the qubit in the superposition state \(\frac{1}{\sqrt{2}}(|1\rangle + |2\rangle)\).

Free evolution

The qubit freely evolves for a time \(t\). A relative phase difference, \(\delta\), accumulates between the \(|1\rangle\) and \(|2\rangle\) states, where (in the rotating frame)

\[ \delta(t) = (\omega_{d} - \omega_{q12})t, \]

and \(\omega_{d}\) and \(\omega_{q12}\) are the microwave drive frequency and qubit resonance frequency between the first and second excited states, respectively. The final state of the qubit at time \(t\) is given by

\[ \frac{1}{\sqrt{2}}(|1\rangle + e^{-t/T_{2, 12}^*}e^{i \delta(t)}|2\rangle). \]

Here, \(e^{-t/T_{2, 12}^*}\) represents the loss of coherence (dephasing) of the 1-2 superposition over time.

\(-\frac{\pi}{2}\)-pulse (\(R_{12}\!\left(-\frac{\pi}{2}\right)\))

A \(-\frac{\pi}{2}\)-pulse resonant with the 1-2 transition is applied after time \(t\). This projects the accumulated phase information onto the population basis (\(|1\rangle\) vs \(|2\rangle\)).

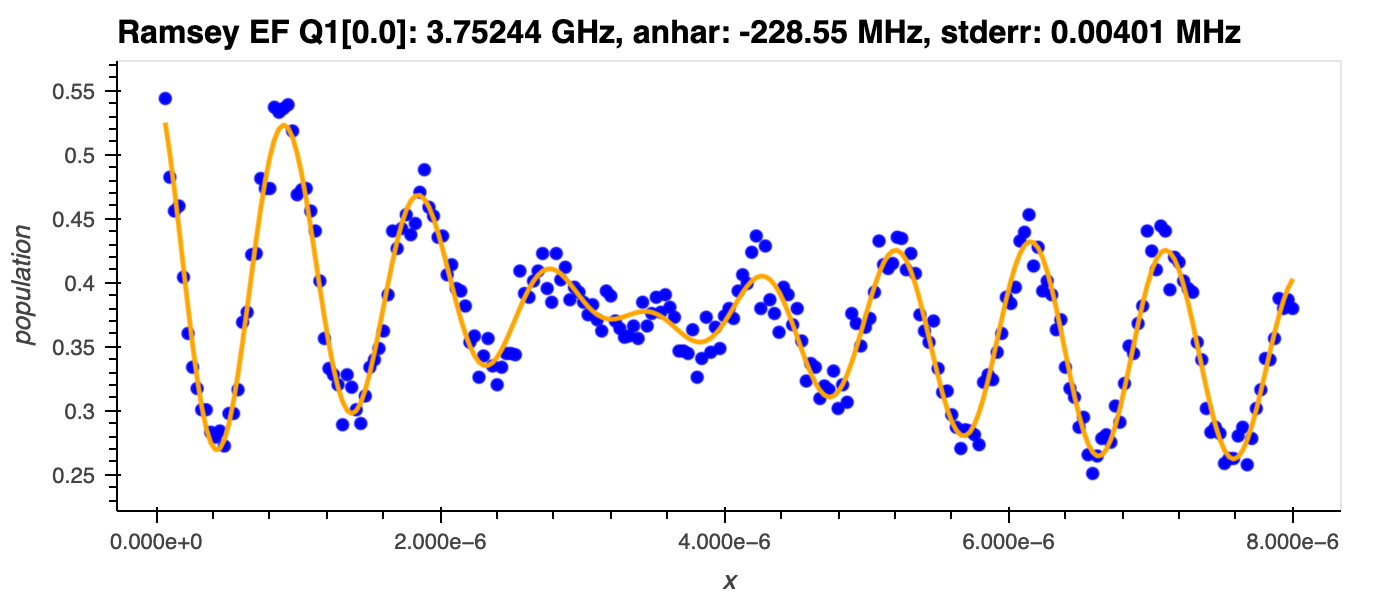
This pulse sequence is then repeated for different values of \(t\). Plotting the amplitude of the resonator signal against \(t\) yields damped oscillations. The frequency of these oscillations corresponds to the detuning \(\Delta_{12} = \omega_{d}-\omega_{q12}\), and the decay envelope corresponds to \(T_{2, 12}^*\).

Experiment steps

1. A \(\pi\)-pulse (\(R_{01}(\pi)\)) is applied to prepare the qubit in the first excited state \(|1\rangle\).

2. A \(\frac{\pi}{2}\)-pulse (\(R_{12}\!\left(\frac{\pi}{2}\right)\)) is applied to create the superposition \(\frac{1}{\sqrt{2}}(|1\rangle + |2\rangle)\).

3. A time \(t\) is waited.

4. A \(-\frac{\pi}{2}\)-pulse (\(R_{12}\!\left(-\frac{\pi}{2}\right)\)) is applied.

5. The resonator transmission is measured.

6. Steps 1 to 5 are repeated for different values of \(t\).

Analysis steps

1. Signal Processing: The amplitude of the readout resonator's signal is calculated as \(\sqrt{I^2 + Q^2}\). Alternatively, the signal can be rotated into a single axis to represent the population probability \(P_{|2\rangle}\) (or depletion of \(P_{|1\rangle}\)).

2. Fitting: The data is plotted against the free evolution time \(t\) and fitted to a damped sinusoidal function:

   \[ f(t) = A e^{-t/T_{2, 12}^*} \cos(2\pi \Delta_{12} t + \phi) + C \]

   where:

   • \(A\): The amplitude of the oscillations.
   • \(\Delta_{12}\): The oscillation frequency, representing the detuning \((\omega_d - \omega_{q12}) / 2\pi\).
   • \(T_{2, 12}^*\): The dephasing time for the 1-2 transition.
   • \(\phi\): The phase offset.
   • \(C\): The vertical offset.

3. Extraction:

   • Frequency correction: The 1-2 transition frequency is updated using the fitted detuning \(\Delta_{12}\). $$ \omega_{q12, \text{new}} = \omega_{d} - 2\pi\Delta_{12} $$
   • Anharmonicity: Using the accurate \(\omega_{q01}\) from previous experiments and the newly obtained \(\omega_{q12}\), the anharmonicity \(\alpha\) is calculated as \(\alpha = \omega_{q12} - \omega_{q01}\).
   • Coherence time: The parameter \(T_{2, 12}^*\) is extracted directly from the exponential decay term, providing a measure of the coherence time associated with the 1-2 transition including inhomogeneous broadening.