Quantum process tomography (single qubit)

This experiment implements quantum process tomography (QPT) for single-qubit rotations. QPT is a procedure that reconstructs an unknown quantum process from measurement data, serving as a fundamental tool for diagnosing and characterising quantum gates and circuits¹.

Description

A quantum process describes how a quantum state evolves under the influence of a physical operation or circuit. Mathematically, any general quantum process \(\mathcal{E}\) acting on a quantum state \(\rho\) can be written as

\[ \mathcal{E}(\rho) = \sum_j E_j \rho E_j^{\dagger}, \]

where \(\rho\) is the density matrix before the process. The set of Kraus operators \({E_j}\) capture all possible transformations the system can undergo, including noise and decoherence.

In QPT, the goal is to characterise and reconstruct \(\mathcal{E}\) for a given quantum circuit, what we'll call the "target quantum circuit". This is achieved by repeating the circuit many times with different input states and measurement bases.

For quantum process tomography, it's often convenient to express \(\mathcal{E}\) in a fixed operator basis \(\{A_m\}\) — for example, the Pauli matrices and their tensor products — which form a complete basis for all possible single- and multi-qubit operations. \(\mathcal{E}\) can then be written as $$ \mathcal{E}(\rho) = \sum_{mn} \chi_{mn} A_m \rho A_n^{\dagger}, $$ where \(\chi\) is the quantum process matrix whose elements \(\chi_{mn}\) fully describe the effect of the process on the density matrix \(\rho\)². Experimentally, \(\chi\) is easier to determine than \(\mathcal{E}\) because it converts the problem of describing a complex quantum operation into estimating a finite set of measurable coefficients from experimental data. \(\mathcal{E}\) can then be reconstructed from \(\chi\).

Experimental steps

1. Defining the custom_gates needed to perform QPT. We employ custom_r90s + custom\ _r180s. This circuit represents the quantum process circuit we aim to reconstruct.

2. Executing the QuantumProcessTomography experiment, which consists of:

   1. Tomography Circuit: creating a quantum circuit (pt_circuit) for performing tomography on a specified quantum instruction (self.instr = rx_instr). We employ the class ProcessTomography from Qiskit ³, which consists of an experiment to reconstruct the quantum channel from measurement data, returning the target quantum channel for process tomography.

   2. Base Circuit: creating a base quantum circuit (base_circuit) that includes the definitions of gates from custom_gates instructions.

   3. Tomography Circuits: executing the transpiled tomography circuits on a quantum backend.

   4. Retrieve and Format Data: Measuring the resonator transmission and collecting the \(I\) and \(Q\) signals for the qubit and circuit.

Analysis Steps

1. Initializing a ProcessTomography object with the target quantum circuit (target_circ). The tomography is performed using the state vector simulator backend (aer_simulator_statevector) with a specified number of shots (statevector_shots) ³.

2. Setting a random seed and configuring bootstrap** options for the process tomography analysis.

3. Running ProcessTomography, results are stored in pt_experiment_data.

4. Obtaning the \(\chi\) matrix for the target circuit. (Please check, I changed it to chi but you had a XI there.)

5. Applying error mitigation using a composite_discriminator.

6. Updating the experiment data with the sampled mitigated counts.

7. Re-running ProcessTomography with the updated experiment data containing the sampled mitigated counts.

8. Storing measured \(\chi\) matrix and fidelity.

** Bootstrapping is a resampling technique. This method involves the generation of multiple datasets by drawing samples with replacement from the original data. It is used to estimate the distribution of a statistic, providing valuable insights into the variability and uncertainty intrinsic to the data.

---

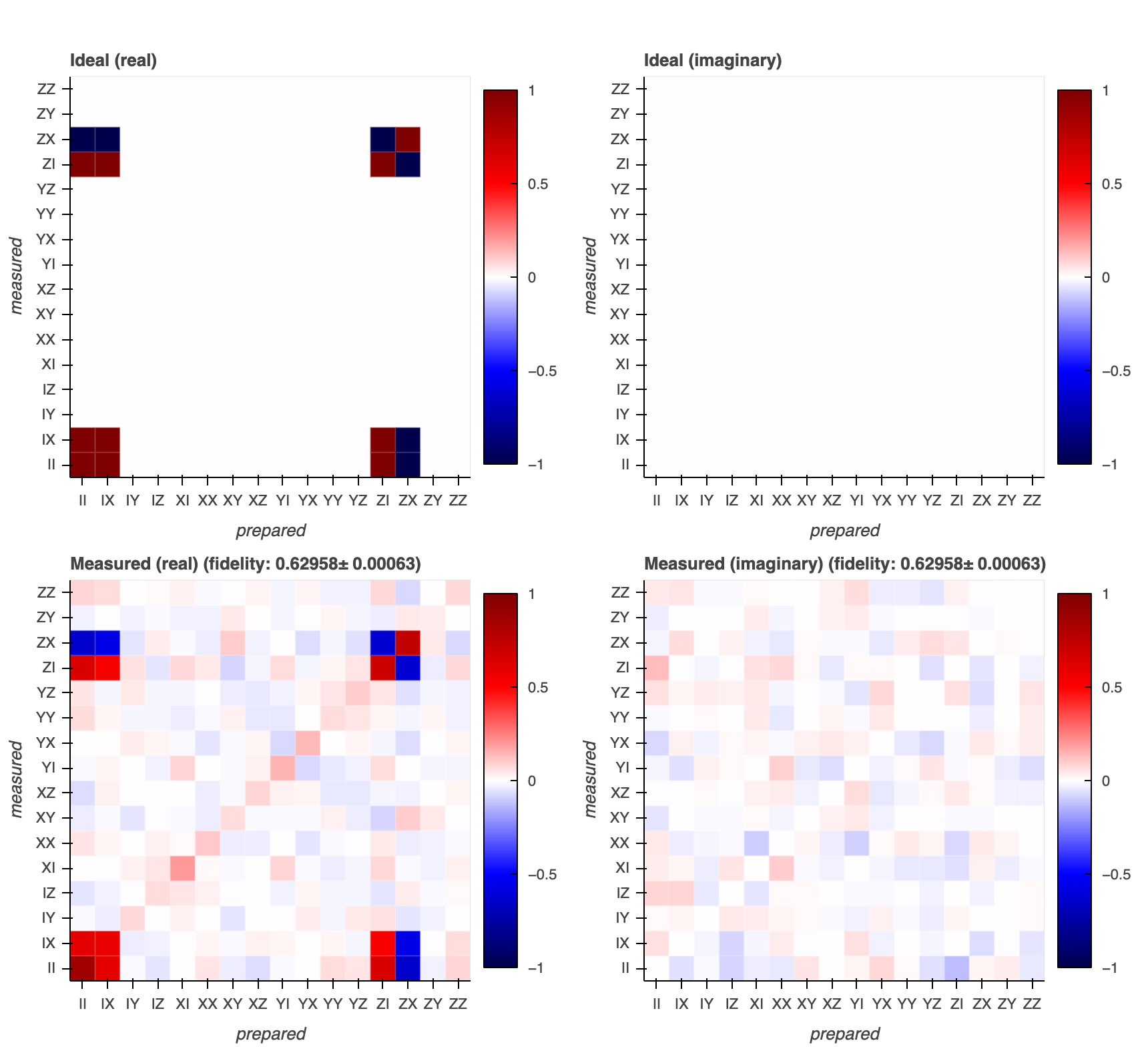1. Michael A. Nielsen and Isaac L. Chuang. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press, 2010. doi:10.1017/CBO9780511976667. ↩

2. Joel Yuen-Zhou, Jacob J Krich, Ivan Kassal, Allan S Johnson, and Alán Aspuru-Guzik. The process matrix and how to determine it: quantum process tomography. In Ultrafast Spectroscopy, 2053-2563, pages 1–1 to 1–9. IOP Publishing, 2014. doi:10.1088/978-0-750-31062-8ch1. ↩

3. Qiskit Experiments. ProcessTomography. Accessed: 2024-06-27. URL: https://qiskit-extensions.github.io/qiskit-experiments/stubs/qiskit_experiments.library.tomography.ProcessTomography.html. ↩↩