ZZ coupling

This experiment measures the residual ZZ coupling (crosstalk) as a function of coupler flux in a qubit-qubit system.

Description

In a cQED system with two coupled transmons, coupling between higher energy levels of the transmons can give rise to residual interactions of the form \(\xi b_{i}^{\dagger} b_{i} b_{j}^{\dagger} b_{j}\), where \(b_{i,j}^{\dagger}\) and \(b_{i,j}\) are the creation and annihilation operators for qubits \(i\) and \(j\) ¹². The parameter \(\xi\), known as the static ZZ crosstalk or residual ZZ coupling, corresponds to the frequency shift of qubit \(i\) depending on the state of qubit \(j\) (and vice versa).

The ZZ coupling can be easily computed by performing a Ramsey experiment on one qubit (say qubit \(i\)) while preparing the other qubit (say qubit \(j\)) in its excited or ground state. In this manner,

\[ \xi = \omega^{j,1}_{i} - \omega^{j,0}_{i} \]

where \(\omega^{j,m}_{i}\) represents the 0-1 frequency of qubit \(i\) when qubit \(j\) is prepared in the state \(|m\rangle = |0\rangle\) or \(|1\rangle\).

It's worth noting that, in a tunable qubit-qubit coupling architecture, \(\xi\) also depends on the coupler flux³. In this experiment, however, we only investigate the ZZ residual coupling with no flux over the coupler. (To determine the ZZ coupling as a function of flux, see the ZZ Coupling Per Flux experiment.)

Experiment steps

1. Qubit \(j\) is prepared in the ground state (\(|m\rangle=|0\rangle\)).

2. A Ramsey sequence is applied to qubit \(i\):

   a. A \(\frac{\pi}{2}\)-pulse (\(R_y(\frac{\pi}{2})\)) is applied, which prepares qubit \(i\) in the superposition state \(\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\).

   b. A time \(t\) (free evolution time) is waited.

   c. A \(-\frac{\pi}{2}\)-pulse (\(R_y(-\frac{\pi}{2})\)) is applied.

   d. The resonator transmission is measured.

   e. Steps a to d are repeated for different values of \(t\).

3. A \(\pi\)-pulse (\(R_x(\pi)\)) is applied to qubit \(j\), preparing it in the excited state (\(|m\rangle=|1\rangle\)).

4. The Ramsey sequence (step 3) is repeated.

Analysis steps

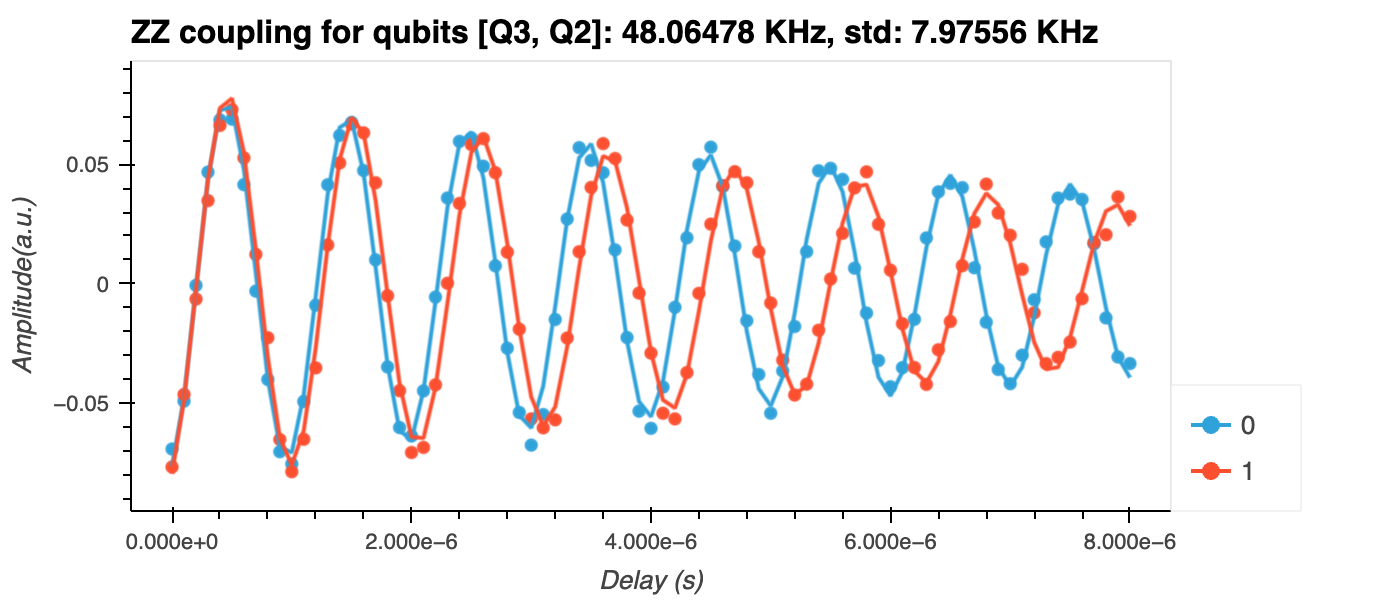
1. The resonator's signal amplitude is computed as a function of the free evolution time, \(t\), when qubit \(j\) is prepared in the state \(|m\rangle=|0\rangle\) and \(m=|1\rangle\). The resonator amplitude is given by \(\sqrt{I^2 + Q^2}\), where \(I\) and \(Q\) are the in-phase and quadrature components of the transmitted signal, respectively.

2. The qubit frequency, \(\omega^{j,m}_{i}\), is determined by fitting the function

   \[ f(t) = A \cos((\omega_d-\omega^{j,m}_{i}) t + \phi) e^{-\Gamma t} + C \]

   to a plot of the resonator amplitude versus delay for each value of \(m\) (figure below).

3. The ZZ coupling is determined as \(\xi = \omega^{j,1}_{i} - \omega^{j,0}_{i}\).

---

1. Pranav Mundada, Gengyan Zhang, Thomas Hazard, and Andrew Houck. Suppression of qubit crosstalk in a tunable coupling superconducting circuit. Phys. Rev. Appl., 12:054023, Nov 2019. doi:10.1103/PhysRevApplied.12.054023. ↩

2. Youngkyu Sung, Leon Ding, Jochen Braumüller, Antti Vepsäläinen, Bharath Kannan, Morten Kjaergaard, Ami Greene, Gabriel O. Samach, Chris McNally, David Kim, Alexander Melville, Bethany M. Niedzielski, Mollie E. Schwartz, Jonilyn L. Yoder, Terry P. Orlando, Simon Gustavsson, and William D. Oliver. Realization of high-fidelity cz and \(zz\)-free iswap gates with a tunable coupler. Phys. Rev. X, 11:021058, Jun 2021. doi:10.1103/PhysRevX.11.021058. ↩

3. Fei Yan, Philip Krantz, Youngkyu Sung, Morten Kjaergaard, Daniel L. Campbell, Terry P. Orlando, Simon Gustavsson, and William D. Oliver. Tunable coupling scheme for implementing high-fidelity two-qubit gates. Phys. Rev. Appl., 10:054062, Nov 2018. doi:10.1103/PhysRevApplied.10.054062. ↩