Skip to content

\(T_{2}\) - Ramsey sequence

This notebook measures the \(T_2^*\) time by measuring the decay rate from a Ramsey experiment.

Description

Note that this experiment is not based on the population decay, i.e. \(p(t) = \frac{1}{2} \Big(1 - \exp[-\chi(t)]\Big)\). Instead, it relies on Quantum Process Tomography (QPT), where the off-diagonal elements of the density matrix are recovered. Consequently, it is possible to reconstruct the coherence function

\[W(t) = \frac{\langle 0 | \rho(t) | 1 \rangle}{\langle 0 | \rho(0) | 1 \rangle} = \langle e^{-i\phi(t)}\rangle,\]

where \(\phi(t)\) is the integral of the stochastic process \(\xi(t)\) on the interval of \([0, t)\).

Note: QPT is a procedure that reconstructs an unknown quantum process from measurement data, serving as a fundamental tool for diagnosing and characterizing quantum gates and circuits1. Essentially, one can describe the change of \(\rho\) in a discrete time step \(\Delta t\) as a quantum process* \(\mathcal{E}\): \(\rho(t_0) \rightarrow \rho(t_0 + \Delta t) =\mathcal{E}(\rho)\) 2. The procedure to infer \(\mathcal{E}\) is called QPT. It is possible to infer the quantum process because of linearity. If one applies the unknown \(\mathcal{E}\) to a complete basis of a density matrix, then by measuring the output, the process can be determined.

Experiment steps

  1. Applying a Hadamard gate and measuring sigma_x. This step consists of:

    1. Applying a \(\pi/2\)-pulse ( RXGate(x/2) ) to rotate the qubit around the \(x\)-axis. Note that x = x180_ampli-\ tude.

    2. Wait for a time \(t\) (delay).

    3. Applying a \(\pi/2\)-pulse ( RYGate(y/2) ) to rotate the qubit around the \(y\)-axis.

    4. Applying a \(\pi\)-pulse ( RXGate(x) ) to collapse the qubit into one of the states of the computational basis.

    5. Measuring the resonator transmission and collecting the \(I\) and \(Q\) signals.

  2. Applying a Hadamard gate and measuring sigma_y. This step consists of:

    1. Applying a \(\pi/2\)-pulse ( RXGate(x/2) ) to rotate the qubit around the \(x\)-axis. Note that x = x180_ampli-\ tude.

    2. Wait for a time \(t\) (delay).

    3. Appying a \(\pi/2\)-pulse ( RYGate(y/2) ) to rotate the qubit around the \(y\)-axis. Note that x = x180_ampli-\ tude.

    4. Applying a \(\pi\)-pulse ( RXGate(x) ) to collapse the qubit into one of the states of the computational basis.

    5. Measuring the resonator transmission and collecting the \(I\) and \(Q\) signals.

  3. Repeating steps 1. to 2. for different values of delay.

Analysis steps

  1. Converting delay sweeps into time time sweeps of the sequences, i.e., time = delay + x180_duration / 2, with x180_duration the pulse duration of the \(\pi\)-pulse.

  2. Computing the expectation of the Pauli matrices (pauli_expectation) as a function of delay. Here, we predict the qubit state from the \(IQ\) data by applying the discriminator trained in the Readout Discriminator Training experiment. The expectation value of a given Pauli matrix is determined by subtracting the probability of observing the excited state from the probability of observing the ground state when measuring the basis of that specific Pauli matrix. In fact, we compute \(\langle \sigma_ x \rangle\) (data_x) and \(\langle \sigma_y \rangle\) (data_y).

  3. Computing the coherence function \(W\) (coherence), which represents the off-diagonal element of the density matrix. The coherence function is calculated as \(W = \frac{1}{2} (\langle \sigma_x \rangle + i\langle \sigma_y \rangle)\). Here, we only consider the real part of the coherence function (\(\text{Re}(W)\)), assuming that the process is Gaussian, meaning all odd cumulants are identically zero, and therefore, the imaginary part is zero.

  4. Determining \(T^{*}_{2}\) by fitting a strechted function to the experimental trace (coherence versus time). The fitting fuction is \(f(x) = A \,\text{exp}(-(x / \theta) ^ \alpha) + \varphi_{\text{off}}\), with \(\theta = T^{*}_{2}\)

* A general quantum process \(\mathcal{E}\) can be described by a set of Kraus operators \(E_j\): \(E(\rho) = Pj E_j\rho E_j^{†}\).

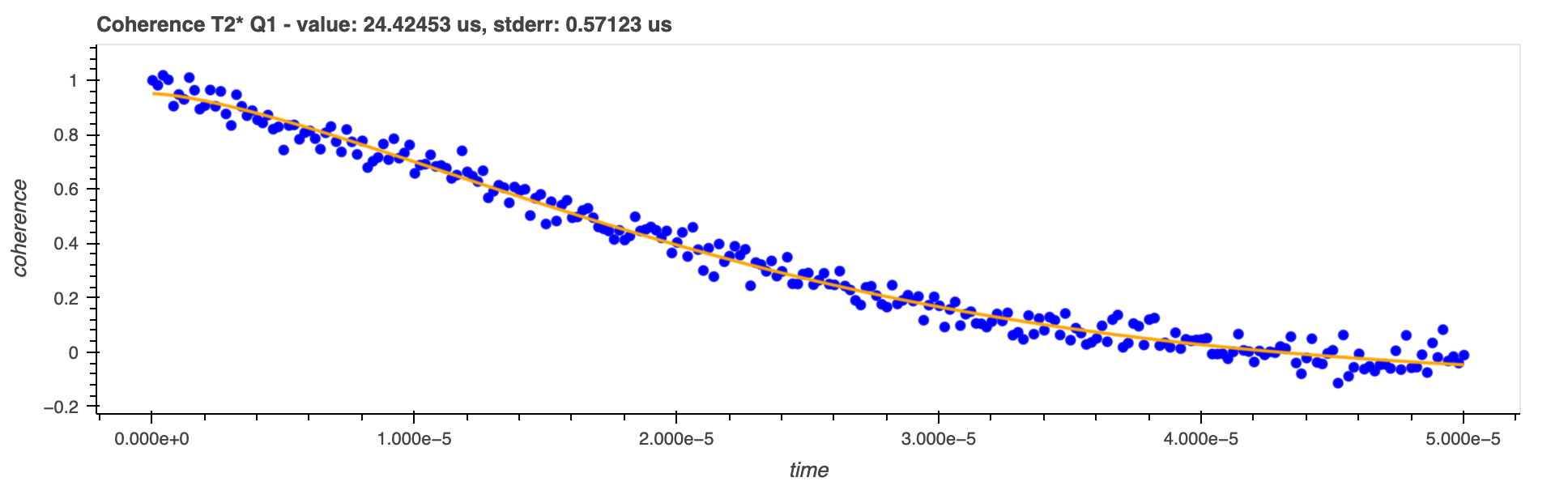
image

  1. Michael A. Nielsen and Isaac L. Chuang. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press, 2010. doi:10.1017/CBO9780511976667. ↩

  2. Yanzhu Chen, Maziar Farahzad, Shinjae Yoo, and Tzu-Chieh Wei. Detector tomography on ibm quantum computers and mitigation of an imperfect measurement. Phys. Rev. A, 100:052315, Nov 2019. doi:10.1103/PhysRevA.100.052315. ↩