\(T_{2}\) echo¶
This experiment measures the dephasing time, \(T_2\), by measuring the decay rate from a Hahn Echo experiment1.
Description¶
The Hahn Echo experiment uses a modified Ramsey sequence with an additional \(\pi\)-pulse placed symmetrically between the \(\frac{\pi}{2}\)-pulses2. The purpose of the \(\pi\)-pulse is to compensate for inhomogeneous broadening that occurs due to low frequency noise in the qubit's environment. Thus, the \(\pi\)-pulse enhances the coherence lifetime and the measured lifetime is \(T_2\), which is generally greater than \(T_2^*\).
Note: the Hahn Echo sequence is the simplest of the dynamical decoupling sequences3.
\(\frac{\pi}{2}\)-pulse
The qubit begins in the ground state and the first \(\frac{\pi}{2}\)-pulse rotates the qubit state around the \(y\)-axis to prepare the superposition state \(\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle)\).
1st free evolution time
The qubit freely evolves for a time \(t\). Generally, we set the detuning between the drive and qubit frequencies to zero (i.e., \(\omega_d-\omega_q=0\)). A relative phase difference between the \(|0\rangle\) and |\(1\rangle\) states, \(\xi(t)\), accumulates due to environmental noise. This corresponds to a rotation of the qubit state around the \(z\)-axis (in the \(xy\)-plane). Assuming the noise is very low frequency, \(\xi(t)\) can be approximated by a random number \(\xi\), and the final state of the qubit at time \(t\) is given by
\(\pi\)-pulse and 2nd free evolution time
A \(\pi\)-pulse around the \(x\)-axis is applied, which effectively flips the qubit so that its new state is
The qubit is again allowed to freely evolve for a time \(t\), accumulating a further relative phase \(\xi\), which brings the \(|0\rangle\) and \(|1\rangle\) states back into phase. In reality, however, noise effects mean that the qubit does not completely rephase. This partial restoration of the coherence is like an "echo" of the original state: very similar in character but received after a delay and with reduced amplitude.
\(-\frac{\pi}{2}\)-pulse
To return the qubit to the measurement basis, a \(-\frac{\pi}{2}\)-pulse rotates the state by \(\frac{\pi}{2}\) around the \(y\)-axis in the opposite direction to the first \(\frac{\pi}{2}\)-pulse. However, due to the small phase accumulated due to noise in the 2nd free evolution, it does not return to \(|0\rangle\). When the readout pulse is applied, the probability of the qubit being in the \(|0\rangle\) or \(|1\rangle\) state is given by the projection onto the \(z\)-axis.
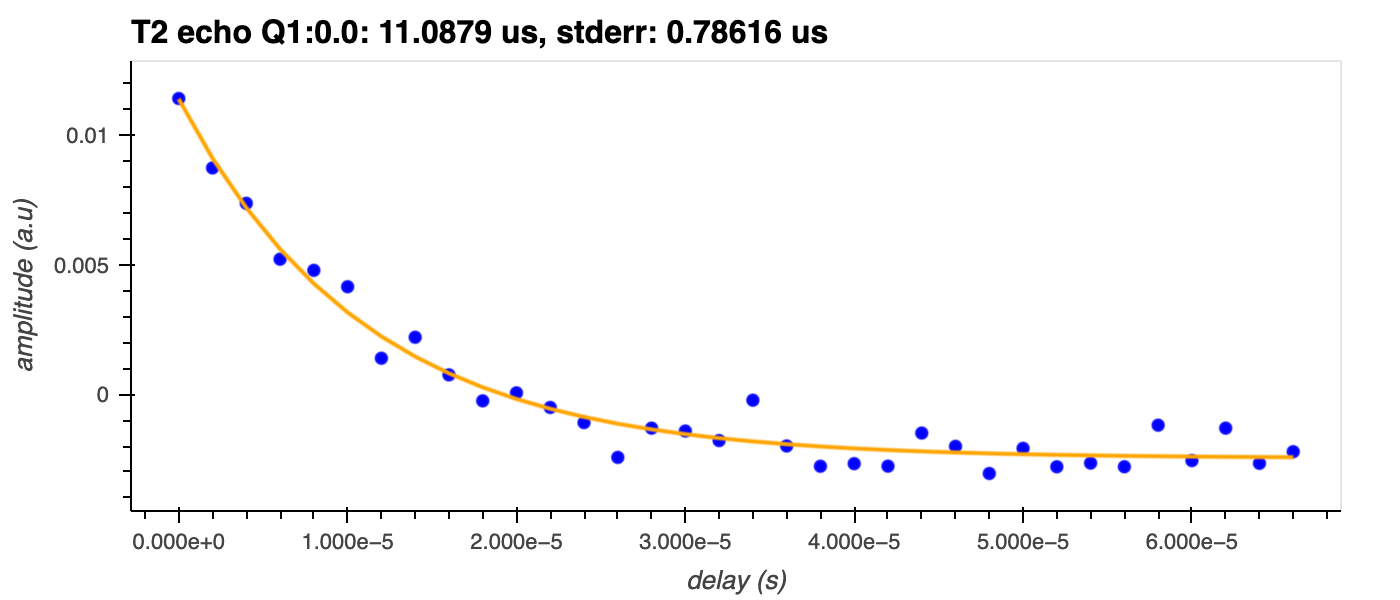
This pulse sequence is then repeated for different values of \(t\) and, when the amplitude of the resonator signal is plotted, an exponential decay is seen.
Experiment steps¶
-
A \(\frac{\pi}{2}\)-pulse (\(R_y(\frac{\pi}{2})\)) is applied, which prepares the qubit in the superposition state \(\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\).
-
A time \(t\) is waited.
-
An intermediate \(\pi\)-pulse (\(R_x(\pi)\)) is applied. This flips the qubit state and reverses the direction of dephasing.
-
A time \(t\) is waited.
-
Another \(\pi/2\)-pulse (\(R_y(\frac{\pi}{2})\)) is applied.
-
The resonator transmission is measured.
-
Steps 1 to 6 are repeated for different values of \(t\).
Analysis steps¶
-
The amplitude of the readout resonator's signal is calculated as \(\sqrt{I^2 + Q^2}\), where \(I\) and \(Q\) are the in-phase and quadrature components of the transmitted signal, respectively.
-
\(T_{2}\) is determined by fitting an exponential decay function to the experimental trace.
-
E. L. Hahn. Spin echoes. Phys. Rev., 80:580–594, Nov 1950. doi:10.1103/PhysRev.80.580. ↩
-
Leigh M. Norris, Gerardo A. Paz-Silva, and Lorenza Viola. Qubit noise spectroscopy for non-gaussian dephasing environments. Phys. Rev. Lett., 116:150503, Apr 2016. doi:10.1103/PhysRevLett.116.150503. ↩
-
Lorenza Viola, Emanuel Knill, and Seth Lloyd. Dynamical decoupling of open quantum systems. Phys. Rev. Lett., 82:2417–2421, Mar 1999. doi:10.1103/PhysRevLett.82.2417. ↩