Skip to content

\(T_{1}\)

This experiment measures the qubit energy relaxation time, \(T_1\).

Description

When left undisturbed, an excited qubit will relax to the ground state at a rate determined by its energy relaxation time1, \(T_1\). To measure \(T_1\) (also known as the longitudinal relaxation time), a \(\pi\)-pulse is applied to prepare the qubit in the excited state (\(|1\rangle\)). The qubit is allowed to decay to its ground state and its state is measured after a variable time delay \(t\). The probability, \(P_{|1\rangle}(t)\), of finding the qubit in the excited state after this time \(t\) is given by

\[ P_{|1\rangle}(t) = P_{|1\rangle}(0) \ \text{e}^{\frac{-t}{T_{1}}}, \]

where \(P_{|1\rangle}(0)\) is the probability of the the qubit being in the excited state immediately after the \(\pi\)-pulse. \(T_1\) can then be extracted from the resulting decay curve.

Experiment steps

  1. A \(\pi\)-pulse (\(R_x(\pi)\)) is applied, which prepares the qubit in the excited state, \(|1\rangle\).

  2. A time \(t\) is waited.

  3. The resonator transmission is measured.

  4. Steps 1 to 3 are repeated for different values of the delay \(t\).

Analysis steps

  1. The amplitude of the readout resonator's signal is calculated as \(\sqrt{I^2 + Q^2}\), where \(I\) and \(Q\) are the in-phase and quadrature components of the transmitted signal, respectively.

  2. The amplitude is plotted against \(t\), and \(T_{1}\) is determined by fitting an exponential function to the experimental trace.

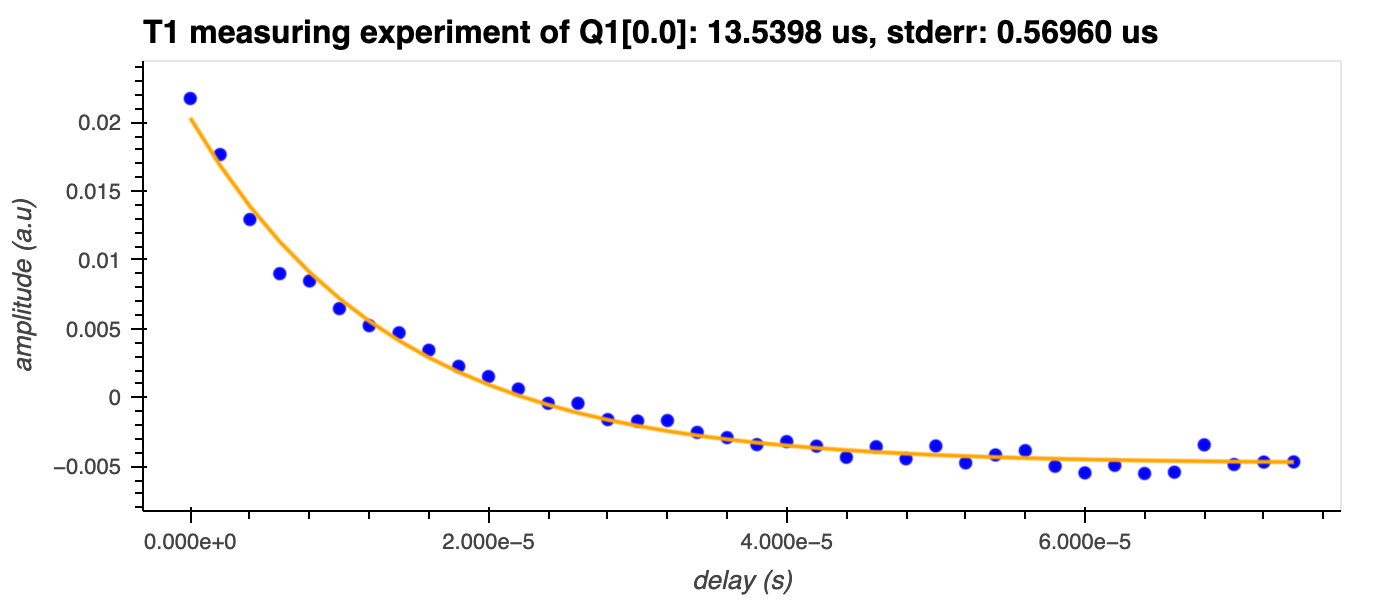
image

  1. Mahdi Naghiloo. Introduction to experimental quantum measurement with superconducting qubits. 2019. arXiv:1904.09291. ↩