Skip to content

Randomised benchmarking

This experiment measures the average single-qubit gate fidelity using randomised benchmarking.

Description

High-fidelity quantum gates are crucial for robust quantum computation. Therefore, benchmarking (determining) the fidelity of these gates is essential for predicting the performance of a quantum computer1.

Randomised benchmarking (RB) protocols include a broad range of techniques that use random circuits of varying lengths to quantify error rates in a gate set. Unlike characterisation techniques such as Quantum Process Tomography (see Cross Resonance Quantum Process Tomography for more details), RB provides a gate (in)fidelity metric that is free of state preparation and measurement (SPAM) errors.

There are many types of RB experiments, each with their own strengths and limitations2. We encourage interested readers to check some of the references below for a deeper dive into RB, but here, we only describe the most standard Clifford-group-based RB.

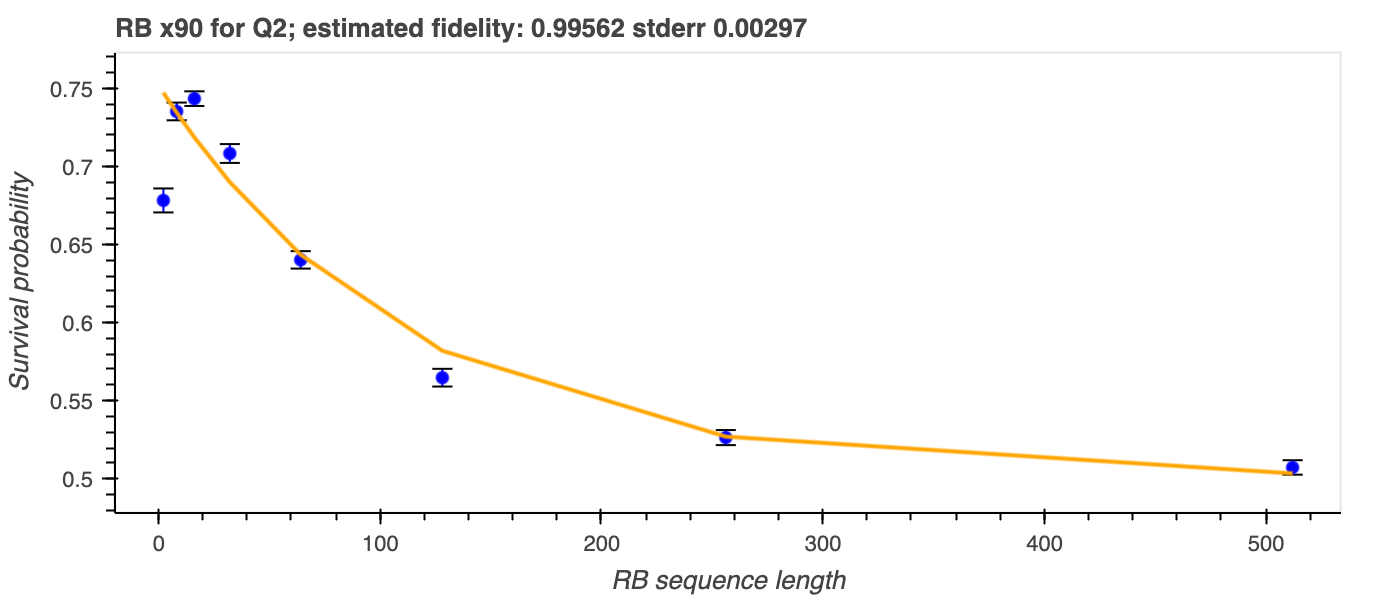
For each RB sequence length \(x\), \(N\) different repetitions are generated by randomising a sequence of the chosen gates. Each sequence is chosen so that the qubit is expected to return to its original state at the end of the sequence. The probability of this happening is known as the average survival probability, \(P_{\text{surv}}\), which is obtained by averaging over all repetitions. This can be fit to an exponential as a function of \(x\) (assuming moderately small Markovian errors):

\[ P_{\text{surv}}(x) = ap^{x} + b , \]

where \(a\), \(p\), and \(b\) are fit parameters.

The average error rate, also called the Error Per Clifford (EPC) or the average gate infidelity, \(r\), can be obtained from \(p\) using the formula

\[ r = 1 - p - \frac{1-p}{2^n} , \]

where \(2^n\) is the Hilbert space spanned by the number of qubits, \(n\).

For \(n=1\) (a single qubit), the average gate fidelity \(\alpha\) or \(1-r\) can be obtained from \(p\) using

\[ \alpha = 1-\frac{(1-p)}{2} . \]

The fit parameters \(a\) and \(b\) are a measure of the SPAM errors, as setting \(x=0\) in the fitted curve provides the fidelities achieved when no gates are applied:

\[ \text{SPAM error} = 1 - (a + b) . \]

Experiment steps

  1. \(N\) different sequences of the same length, \(x\), are defined, each consisting of gates from the set \(R_x(\frac{\pi}{2})\), \(R_x(-\frac{\pi}{2})\), \(R_y(\frac{\pi}{2})\), and \(R_y(-\frac{\pi}{2})\).

  2. The RB sequences are applied to the qubit, which begins in its ground state \(|0\rangle\).

  3. The resonator transmission is measured for each of the \(N\) sequences.

  4. Steps 1 to 3 are repeated for varying lengths of the gate sequence, \(x\).

Two-qubit Randomised Benchmarking

The above instructions are for single-qubit Randomised Benchmarking. When performing two-qubit RB, the only relevant change is the choice of the gateset. Along with the single qubit gates described here, we also include the \(\text{CNOT}\) gate when generating the random RB sequences.

Analysis steps

  1. The qubit state is determined from the \(I\)-\(Q\) data by applying the discriminator trained in the Readout Discriminator Training experiment.

  2. The survival probability, \(P_{\text{surv}}(x)\), is calculated by averaging the probabilities over the number of repetitions, \(N\), of the RB sequence.

  3. The survival probability, \(P_{\text{surv}}(x)\), is plotted against the sequence length, \(x\) (see figure below), and an exponential curve is fit to the data.

  4. The fit parameter \(p\) is used to calculate the average gate fidelity, \(\alpha\).

  5. The fit parameters \(a\) and \(b\) are used to calculate the SPAM error.

image

  1. Matthew James Baldwin. Randomized benchmarking simulations of quantum gate sequences with z-gate virtualization. 2021. URL: https://hdl.handle.net/1721.1/139448. ↩

  2. Akel Hashim, Long B. Nguyen, Noah Goss, Brian Marinelli, Ravi K. Naik, Trevor Chistolini, Jordan Hines, J. P. Marceaux, Yosep Kim, Pranav Gokhale, Teague Tomesh, Senrui Chen, Liang Jiang, Samuele Ferracin, Kenneth Rudinger, Timothy Proctor, Kevin C. Young, Robin Blume-Kohout, and Irfan Siddiqi. A practical introduction to benchmarking and characterization of quantum computers. 2024. arXiv:2408.12064. ↩