Skip to content

Ramsey

This experiment provides a more accurate estimate of the qubit's resonance frequency, \(\omega_q\).

Description

The qubit resonance frequency, \(\omega_q\), determined using Pulsed Qubit Spectroscopy tends to be slightly detuned from its actual value due to finite pulse duration, power broadening, environmental noise, and imperfect fitting of the Lorentzian function1. While this serves as a good first guess for \(\omega_q\), the Ramsey experiment uses the phase evolution of the qubit to obtain a much more precise value.

The pulse sequence for the Ramsey experiment consists of a \(\frac{\pi}{2}\)-pulse followed by a \(-\frac{\pi}{2}\)-pulse, with a free evolution of the qubit between the two pulses.

\(\frac{\pi}{2}\)-pulse

The qubit begins in the ground state and the first \(\frac{\pi}{2}\)-pulse prepares the qubit in the superposition state \(\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\).

Free evolution

The qubit freely evolves for a time \(t\). A relative phase difference, \(\delta\), accumulates between the \(|0\rangle\) and \(|1\rangle\) states, where (in the rotating frame)

\[ \delta = (\omega_{d} - \omega_{q})t, \]

and \(\omega_{d}\) and \(\omega_{q}\) are the microwave drive frequency and qubit resonance frequency, respectively. This corresponds to a rotation of the qubit state around the \(z\)-axis (in the \(xy\)-plane). The final state of the qubit at time \(t\) is given by

\[ \frac{1}{\sqrt{2}}(|0\rangle + e^{i \delta}|1\rangle). \]

\(-\frac{\pi}{2}\)-pulse

A \(-\frac{\pi}{2}\)-pulse is applied after time \(t\), rotating the state by \(\frac{\pi}{2}\) around the \(x\)-axis in the opposite direction to the first pulse. This returns the qubit to the measurement basis. However, due to the accumulated phase, \(\delta\), it does not return to \(|0\rangle\). When the readout pulse is applied, the probability of the qubit being in the \(|0\rangle\) or \(|1\rangle\) state is given by the projection onto the \(z\)-axis.

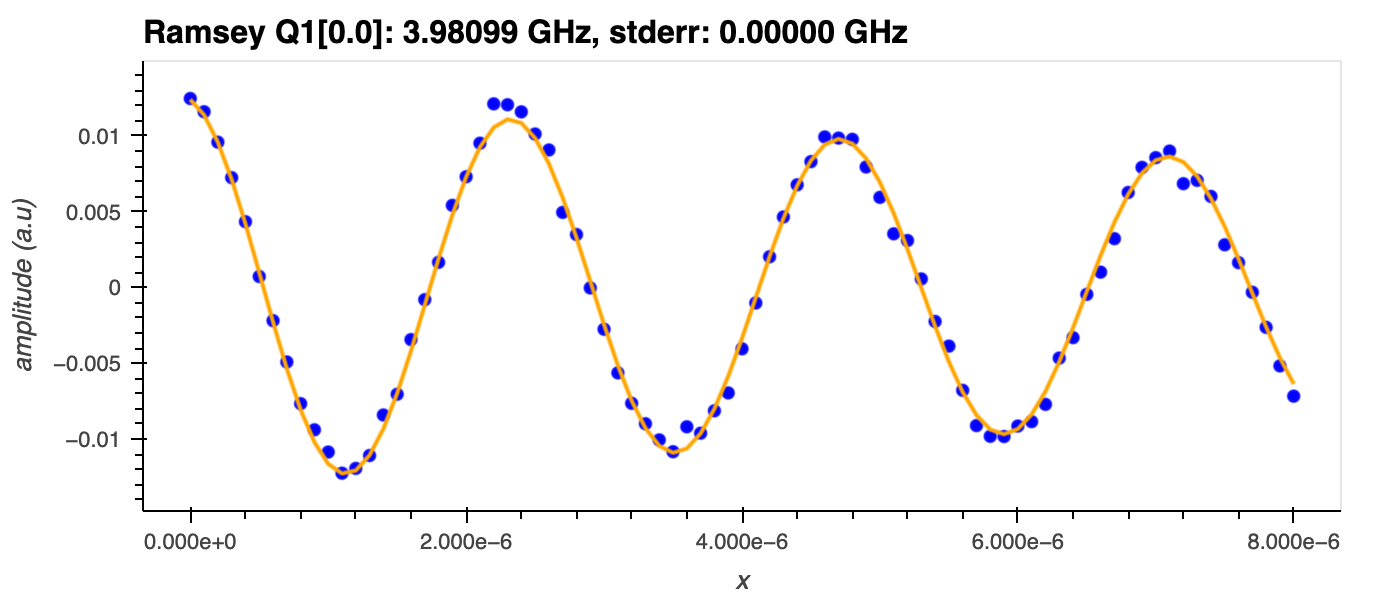
This pulse sequence is then repeated for different values of \(t\). Plotting the amplitude of the resonator signal against \(t\) yields damped oscillations with frequency \(\delta=\omega_{d}-\omega_{q}\) (see figure below). These can be described by

\[ f(t) = A \cos((\omega_{d}-\omega_{q}) t + \phi) e^{-\Gamma t} + C , \]

where \(A\) and \(\phi\) are the initial amplitude and phase of the oscillations, respectively, and \(C\) is an offset constant. The decay rate, \(\Gamma\), arises from additional dephasing of the superposition due to the qubit interacting with its surrounding environment. \(\omega_q\) can be extracted from a fit of \(f(t)\) to the data.

Experiment steps

  1. A \(\frac{\pi}{2}\)-pulse (\(R_y(\frac{\pi}{2})\)) is applied, which prepares the qubit in the superposition state \(\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\).

  2. A time time \(t\) is waited.

  3. A \(-\frac{\pi}{2}\)-pulse (\(R_y(-\frac{\pi}{2})\)) is applied.

  4. The resonator transmission is measured.

  5. Steps 1 to 4 are repeated for different values of \(t\).

Analysis steps

  1. The amplitude of the filter resonator's signal is calculated as \(\sqrt{I^2 + Q^2}\), where \(I\) and \(Q\) are the in-phase and quadrature components of the transmitted signal, respectively.

  2. This amplitude is plotted against \(t\) (free evolution time), and the function, \(f(t)\), which describes damped oscillations, is fit to the data. \(\omega_q\) is then extracted from the fit.

image

  1. Mahdi Naghiloo. Introduction to experimental quantum measurement with superconducting qubits. 2019. arXiv:1904.09291. ↩