Flux crosstalk calibration¶
This experiment measures the flux crosstalk between two qubits.
Description¶
Superconducting circuits employ magnetic fluxes to tune the frequency of qubits (see Pulsed Qubit Spectroscopy per Flux). In these architectures, the current used to generate flux in one qubit's SQUID loop may result in spurious fluxes that influence neighbouring qubits; this is known as flux crosstalk1.
Given two coupled qubits, crosstalk quantifies the flux, \(\Phi_{T}\), experienced by the target qubit given an adversarial flux \(\Phi_{N}\) applied to the neighbour qubit. In other words, crosstalk is defined as
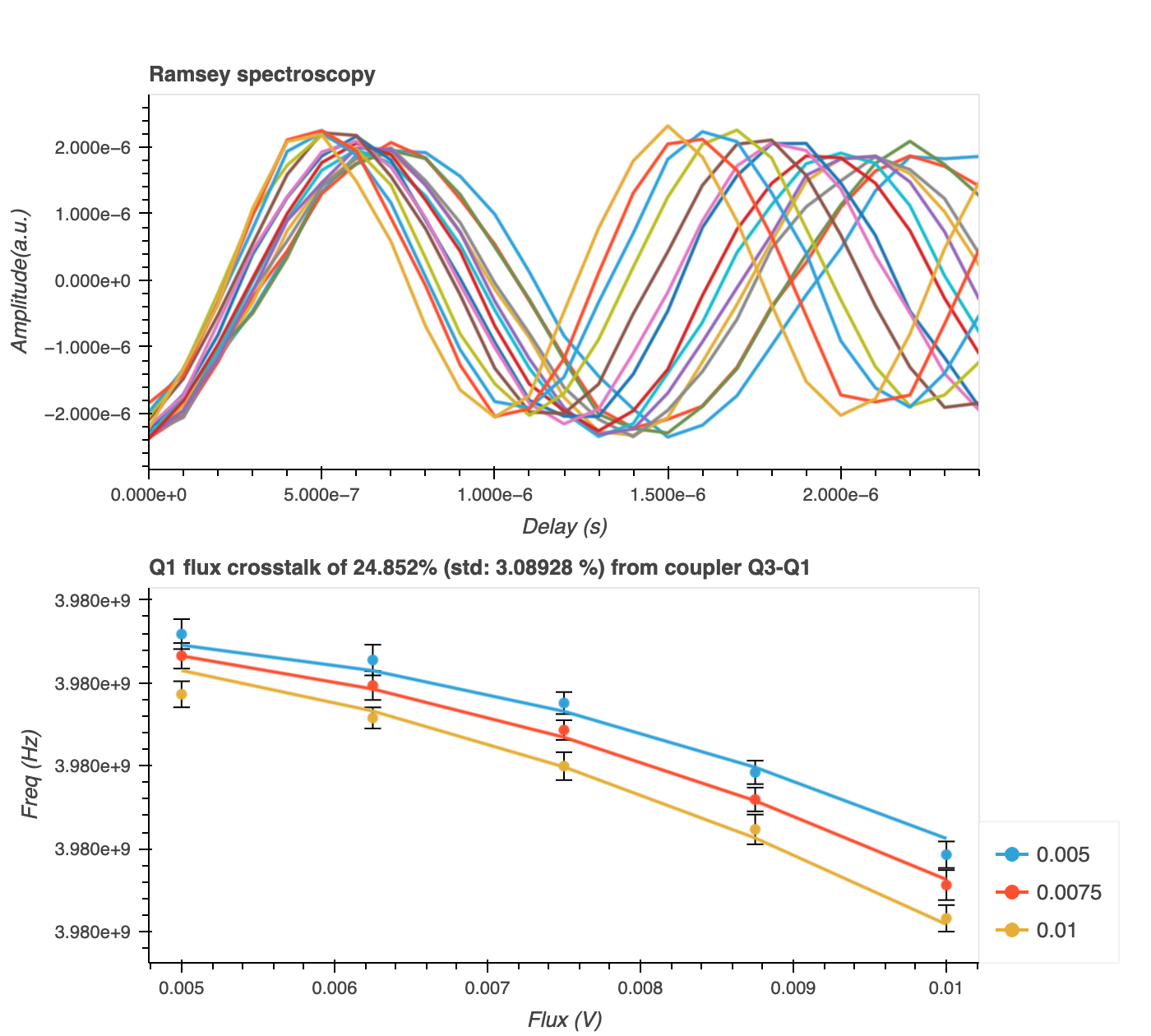
In this experiment, we implement a Ramsey experiment while applying a flux bias to a neighbouring qubit. During the wait time between the two \(\frac{\pi}{2}\)-pulses, some flux reaches the target qubit and modifies its frequency. The Ramsey sequence detects this frequency shift, allowing us to determine the impact of the neighbouring qubit’s flux on the target qubit.
Experimental steps¶
-
The target qubit is flux-biased to enhance the observation of crosstalk effects, which exhibit quadratic dependence (i.e., small changes in flux can cause significant variations in crosstalk).
-
The neighbouring qubit is flux-biased at higher values to enhance crosstalk effects on the target qubit.
-
A Ramsey sequence is applied:
a. A \(\frac{\pi}{2}\)-pulse (\(R_y(\frac{\pi}{2})\)) is applied, which prepares the target qubit in the superposition state \(\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\).
b. A time \(t\) (free evolution time) is waited.
c. A \(-\frac{\pi}{2}\)-pulse (\(R_y(-\frac{\pi}{2})\)) is applied.
d. The resonator transmission is measured.
e. Steps a to d are repeated for different values of \(t\).
-
The Ramsey sequence (step 3) is repeated for different combinations of flux values applied to the target and neighbouring qubits.
Analysis steps¶
-
A Ramsey Analysis is performed for each combination of flux values applied to the target and neighbouring qubits:
a. The amplitude of the filter resonator's signal is calculated as \(\sqrt{I^2 + Q^2}\), where \(I\) and \(Q\) are the in-phase and quadrature components of the transmitted signal, respectively.
b. This amplitude is plotted against the free evolution time, \(t\) (top panel in figure below), and the function
\[ f(t) = A \cos((\omega_d-\omega_{qT}) t + \phi) e^{-\Gamma t} + C, \]which describes damped oscillations, is fit to the data (see the Ramsey experiment for more details). The target qubit frequency, \(\omega_{qT}\), is then extracted from the fit.
-
To calculate the crosstalk, a polynomial function is fit to a plot of \(\omega_{qT}\) against flux applied to the target qubit, \(\Phi\), for each value of flux applied to the neighbouring qubit, \(\Phi_N\) (bottom panel in figure below). We employ a quadratic approximation to obtain the effective flux, \(\Phi_{T}\), over the target qubit:
\[ f(t) = a \Phi_{T}^2 + b \Phi_{T} + c, \]where \(\Phi_{T} = \Phi + X_{\Phi} \Phi_{N}\). The crosstalk coefficient, \(X_\Phi\), can then be extracted.
-
Deanna M. Abrams, Nicolas Didier, Shane A. Caldwell, Blake R. Johnson, and Colm A. Ryan. Methods for measuring magnetic flux crosstalk between tunable transmons. Phys. Rev. Appl., 12(6):064022, Dec 2019. doi:10.1103/PhysRevApplied.12.064022. ↩