Cross resonance quantum process tomography¶
The notebook implements QPT for a cross resonance gate.
Description¶
Quantum process tomography (QPT) is a procedure that reconstructs an unknown quantum process from measurement data, serving as a fundamental tool for diagnosing and characterizing quantum gates and circuits1. Essentially, it is possible to describe the change of \(\rho\) in a discrete-time step \(\Delta t\) as a quantum process* \(\mathcal{E}\): \(\rho(t_0) \rightarrow \rho(t_0 + \Delta t) =\mathcal{E}(\rho)\). The procedure to infer \(\mathcal{E}\) is called QPT 2.
In QPT, the goal is to characterise and reconstruct the quantum channel that describes the evolution of a quantum system under the influence of a particular circuit. The quantum channel is a mathematical representation of the transformation applied to a quantum state. One possible representation is achieved through the 'superoperator' \(\chi\) known as the quantum process matrix3, being a linear operator within the space of density matrices. \(\chi\) captures the action of the quantum channel on a density matrix, which represents the state of a quantum system, and its reconstruction via a finite number of experiments is the main goal of QPT. The Chi matrix \(\xi\) is defined as:
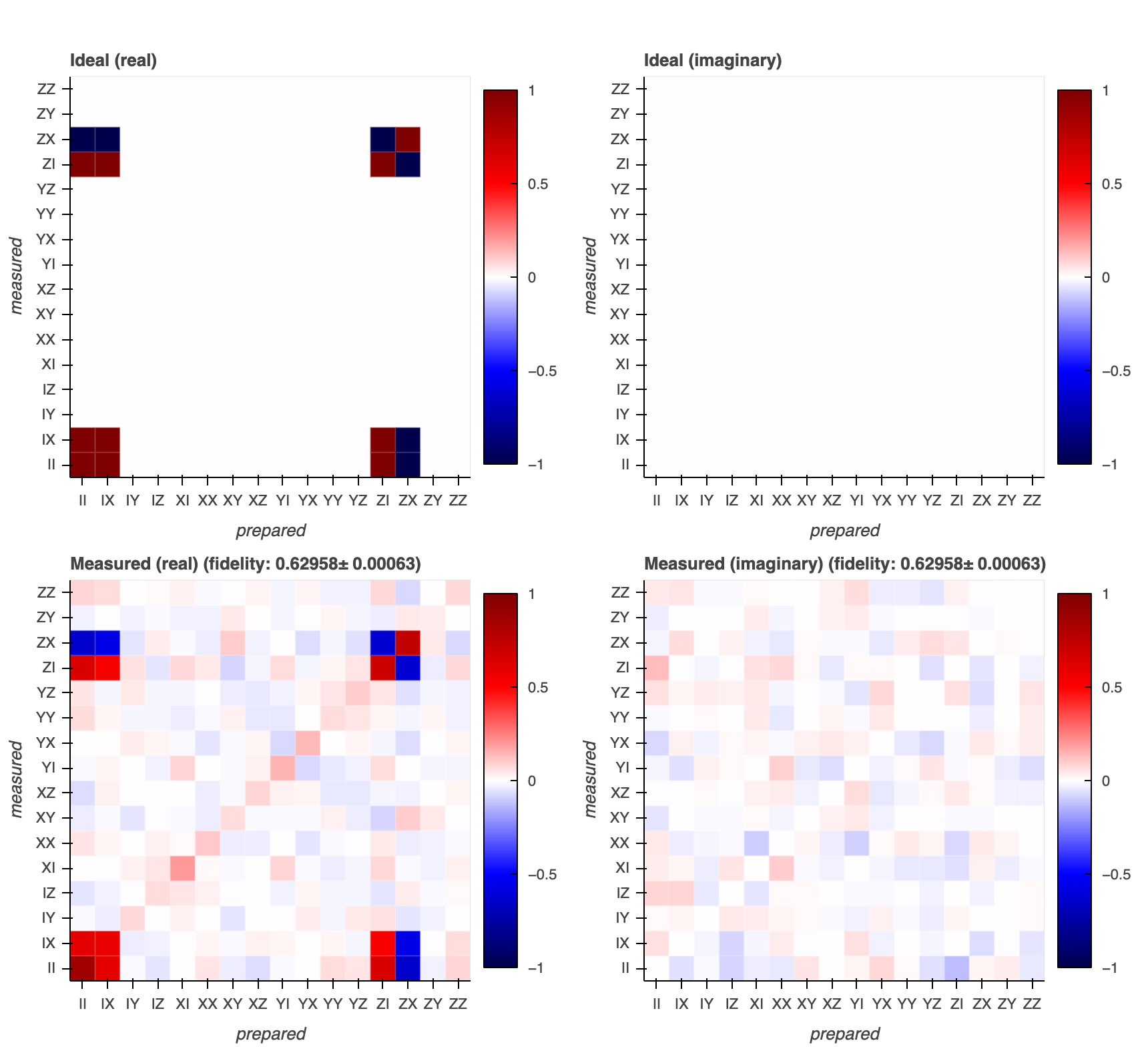
Along these lines, this notebook implements QPT for a cross resonance gate. Refer to the Cross Resonance Amplitude Sweep experiment for further details.
Experimental steps¶
-
Defining the
custom_gatesneeded to perform cross-resonance QPT. We employcustom_r90s + custom\_r180s. This circuit represents the quantum process circuit we aim to reconstruct. -
Executing the
QuantumProcessTomographyexperiment, which consists of:-
Tomography Circuit: creating a quantum circuit (
pt_circuit) for performing tomography on a specified quantum instruction (self.instr=zx_instr). We employ the classProcessTomographyfrom Qiskit 4, which consists of an experiment to reconstruct the quantum channel from measurement data, returning the target quantum channel for process tomography. -
Base Circuit: creating a base quantum circuit (
base_circuit) that includes the definitions of gates fromcustom_gatesinstructions. -
Tomography Circuits: executing the transpiled tomography circuits on a quantum backend.
-
Retrieve and Format Data: Measuring the resonator transmission and collecting the \(I\) and \(Q\) signals for each qubit and circuit.
-
Analysis steps¶
-
Initializing a
ProcessTomographyobject with the target quantum circuit (target_circ). The tomography is performed using the state vector simulator backend (aer_simulator_statevector) with a specified number of shots (statevector_shots) 4. -
Setting a random seed and configuring bootstrap** options for the process tomography analysis.
-
Running
ProcessTomography, results are stored inpt_experiment_data. -
Obtaning the \(\Xi\) matrix for the target circuit.
-
Applying error mitigation using a
composite_discriminator. -
Updating the experiment data with the sampled mitigated counts.
-
Re-running
ProcessTomographywith the updated experiment data containing the sampled mitigated counts. -
Storing measured \(\chi\) matrix and fidelity.
* A general quantum process \(\mathcal{E}\) can be described by a set of Kraus operators, \(E_j\), such that \(E(\rho) = Pj E_j\rho E_j^{†}\).
** Bootstrapping is a resampling technique. This method involves the generation of multiple datasets by drawing samples with replacement from the original data. It is used to estimate the distribution of a statistic, providing valuable insights into the variability and uncertainty intrinsic to the data.
-
Michael A. Nielsen and Isaac L. Chuang. Quantum Computation and Quantum Information: 10th Anniversary Edition. Cambridge University Press, 2010. doi:10.1017/CBO9780511976667. ↩
-
Yanzhu Chen, Maziar Farahzad, Shinjae Yoo, and Tzu-Chieh Wei. Detector tomography on ibm quantum computers and mitigation of an imperfect measurement. Phys. Rev. A, 100:052315, Nov 2019. doi:10.1103/PhysRevA.100.052315. ↩
-
Joel Yuen-Zhou, Jacob J Krich, Ivan Kassal, Allan S Johnson, and Alán Aspuru-Guzik. The process matrix and how to determine it: quantum process tomography. In Ultrafast Spectroscopy, 2053-2563, pages 1–1 to 1–9. IOP Publishing, 2014. doi:10.1088/978-0-750-31062-8ch1. ↩
-
Qiskit Experiments. ProcessTomography. Accessed: 2024-06-27. URL: https://qiskit-extensions.github.io/qiskit-experiments/stubs/qiskit_experiments.library.tomography.ProcessTomography.html. ↩↩