Skip to content

Cross-resonance pulse duration

The notebook implements cross-resonance tomography with a smaller time step, allowing for a more precise determination of the gate duration.

Description

As explained in the Cross Resonance Amplitude Sweep, two-qubit entangling operations can be realized using a microwave-activated cross-resonance interaction12. This interaction is enabled by applying a cross-resonant drive tone, corresponding to a qubit drive resonant with a neighboring qubit's transition. The local drive on one qubit (\(Q_C\), the control qubit), resonant with the first transition frequency of the other qubit (\(Q_T\), the target qubit), introduces an interaction between them. The interaction Hamiltonian depends on the cross-resonance pulse amplitude, \(\Omega_{12}\), but also on its phase.

In this notebook, we implement cross-resonance tomography with a smaller time step to more precisely determine the gate duration.

For more theoretical details, please refer to the Cross Resonance Amplitude Sweep experiment.

Experimental steps

  1. Defining the circuits needed to perform cross-resonance tomography, the method _build_single_qubit_instructions inside the class CrossResonanceTomography receives qubit characterization and constructs a dictionary containing three key-value pairs:

    1. ctrl_rx180p: It creates a gate instruction named rx180p for the control qubit. The frequency is set to the value obtained from the characterization.

    2. target_rx90p: It creates a gate instruction named rx90p for the target qubit. The frequency is set to the value obtained from the characterization, and the xy_angle is set to 0.

    3. target_ry90m: It creates a gate instruction named ry90m for the target qubit. The frequency is set to the value obtained from the characterization, and the xy_angle is set to -np.pi / 2.

  2. For each pair of the control qubit states (0-1 states) and expectation values in the \(\sigma_x\), \(\sigma_y\), and \(\sigma_z\) bases, denoted as (ctrl_state, exp_val), we perform a CrossResonanceTomography:

    1. If ctrl_state == 1, append ctrl_rx180p.

    2. Applying a cr_pulse (\(\hat{ZX}\)):

      • If we set echo=True, cr_pulse consists of an echo-gate scheme (to reduce errors in the calibration, a cancellation tone can be applied [3]). A \(\hat{ZX}\) gate can be formed with two rx180 gates on the control qubit.

      • If we set echo=False, cr_pulse consists of a ctrl_rx180p pulse.

    3. Measuring the resonator transmission and collect the \(I\) and \(Q\) signals:

      • Applying target_ry90m to measure the qubit in the \(\sigma_x\)-basis.

      • Applying target_rx90p to measure the qubit in the \(\sigma_y\)-basis.

      • No extra pulse is applied to measure the qubit in the \(\sigma_z\)-basis.

Analysis steps

  1. Computing the resonator's amplitude (amplitude) signal as a function of pulse_lengths. Here, we predict the qubit state from the \(IQ\) data by applying the composite_discriminator obtained in the Correlated Readout Error experiment.

  2. Computing the expectation_values (omega_x, omega_y, omega_z) in the (\(\sigma_x\), \(\sigma_y\), \(\sigma_z\)) basis using the populations obtained in step 1.

  3. Computing the off-resonant control qubit drive terms, cross-resonance interaction terms, and rotations on the target qubit (hamiltonian_param), i.e., ["IX", "IY", "IZ", "ZX", "ZY", "ZZ"]. We utilize the fit_\ cross_resonance_curves function, employing the cr_propagator and propagate_state functions to simulate quantum states based on the input parameters (omega_x, omega_y, omega_z) from 2. On one hand, cr_propagator calculates the propagator for a quantum gate corresponding to the cross-resonance interaction over a small time interval. It constructs a 3x3 matrix generator based on the input angular frequencies (omega_x, omega_y, omega_z) and returns the matrix exponential of the generator matrix multiplied by the time step dt. On the other hand, propagate_state iteratively applies the previous propagator to the initial state at each time point in the list ts (pulse_lengths).

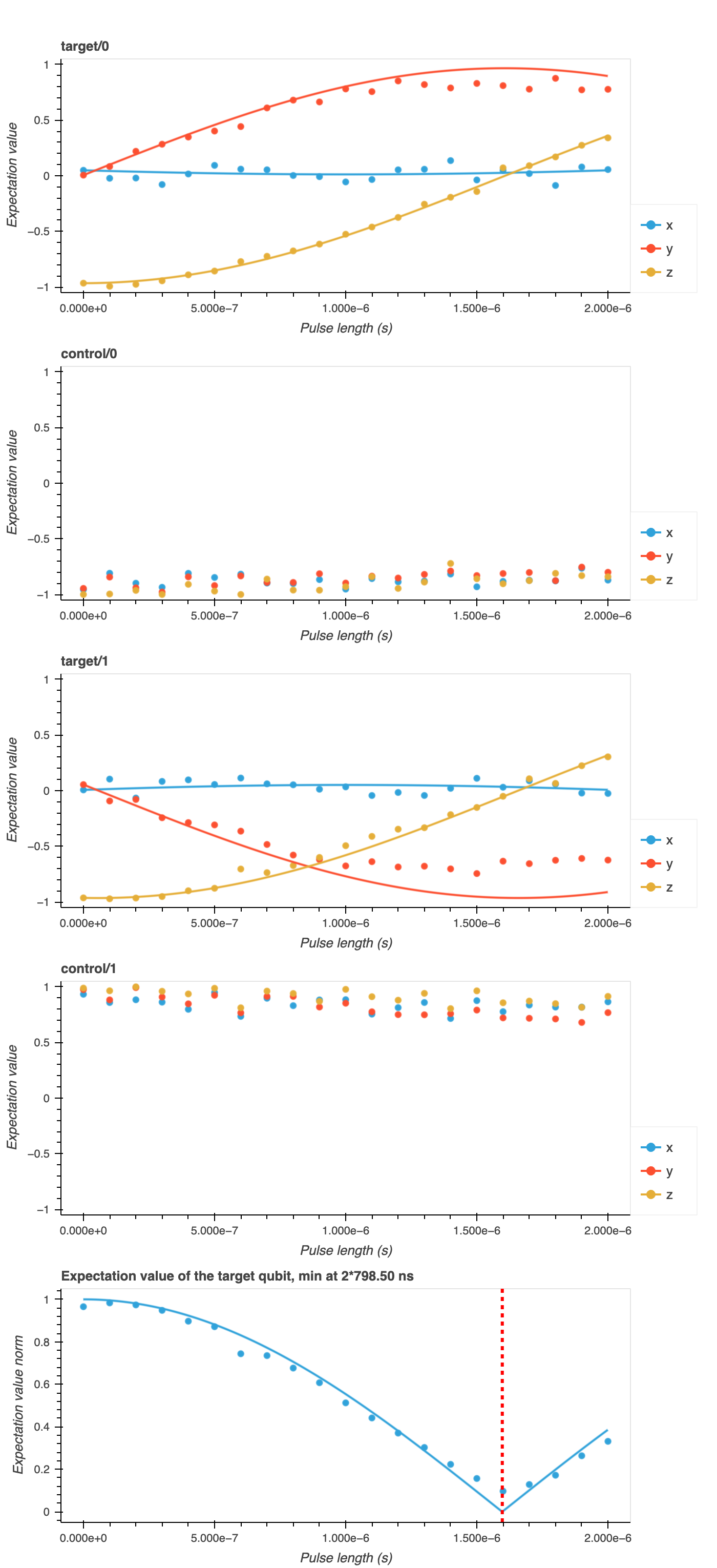
image

  1. Chad Rigetti and Michel Devoret. Fully microwave-tunable universal gates in superconducting qubits with linear couplings and fixed transition frequencies. Phys. Rev. B, 81:134507, Apr 2010. doi:10.1103/PhysRevB.81.134507. ↩

  2. A.D. Patterson, J. Rahamim, T. Tsunoda, P.A. Spring, S. Jebari, K. Ratter, M. Mergenthaler, G. Tancredi, B. Vlastakis, M. Esposito, and P.J. Leek. Calibration of a cross-resonance two-qubit gate between directly coupled transmons. Phys. Rev. Appl., 12:064013, Dec 2019. doi:10.1103/PhysRevApplied.12.064013. ↩