Skip to content

Calibrate \(\pi\) amplitude with ping-pong (1-2 states)

This notebook uses ping-pong to calibrate amplitude \(\pi\) gates by sweeping the amplitude while repeating a gate multiple times.

Description

Precisely estimating a small error on a control parameter requires a technique that can selectively amplify the error of interest. The ping-pong technique is an experimental error amplification procedure designed to correct over- or under-rotations in single-qubit gates12.

In this notebook, the sequence used to drive the qubit is \([\pi/2\)-pulse - \([\pi_{12}\)-pulse \(]^{n}]\), where \(n\) is the number of repetitions and \(\pi\)-pulse is the previously calibrated gate for the 01 transition while \(\pi_{12}\)-pulse is the gate for the 12 transition which we have roughly calibrated via a Rabi amplitude experiment for the 12 transition. The resulting qubit populations \(P(|g\rangle)\) (\(P(|0\rangle)\)) as a function of pulse amplitude \(x\) and \(n\) roughly follow the relation

\(f(x, n) = -a \cos(x(\theta + \varphi_{\text{gate}}) n + \varphi_{0}) + b\).

Here, \(\theta\) is the parameter to fit, used to compute a precise estimate of the \(\pi_{12}\)-amplitude.

Experiment steps

  1. Applying the sequence \([\pi/2\)-pulse - \([\pi_{12}\)-pulse \(]^{n}]\) (char.x90 - [char.x180_ef]\(^{n}\)) to the qubit while sweeping the \(\pi_{12}\)-amplitude (x180_ef_amplitude) over a range of values defined around the expected amplitude, as specified in the qubit parameters (char.x180_ef.amplitude).

  2. Measuring the resonator transmission and collecting the \(I\) and \(Q\) signals for each value of x180_ef_amplitude.

  3. Repeating steps 1 and 2, increasing the number of repetitions \(n\).

Analysis steps

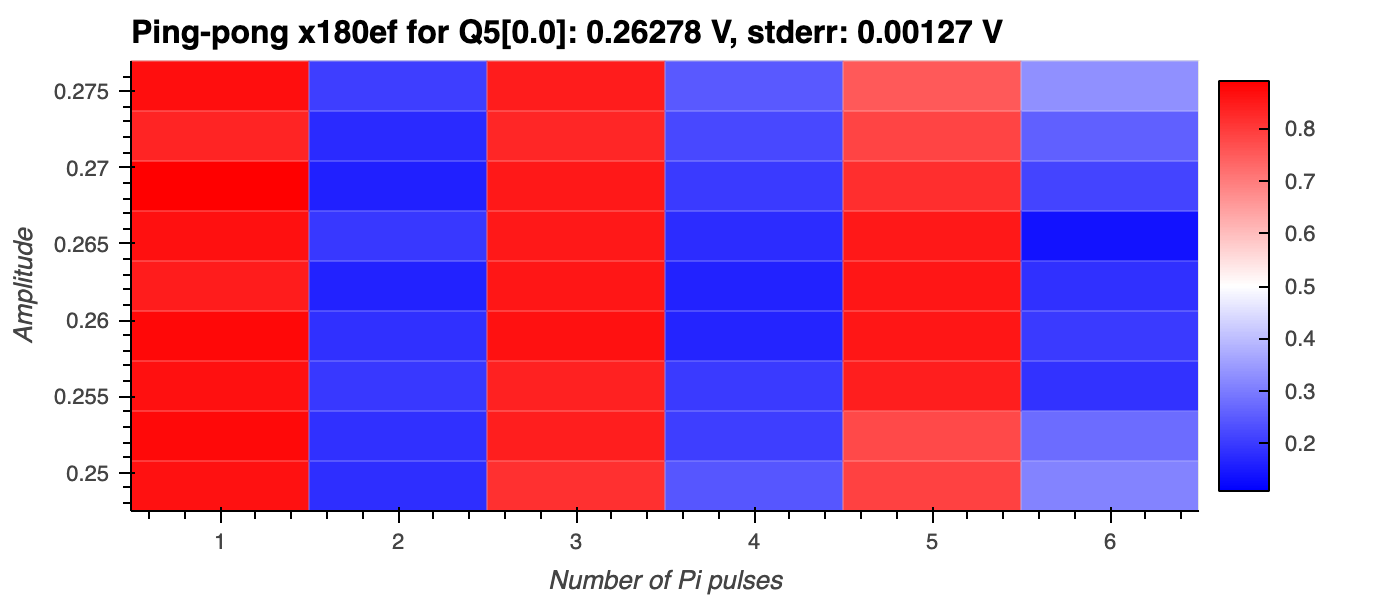
  1. Computing the resonator's amplitude (amplitude) signal as a function of the number \(n\) of \(\pi_{12}\)-pulses (Number of Pi pulses) and \(\pi_{12}\)-amplitude (x180_ef_amplitude). Here, we predict the qubit state from the \(IQ\) data by applying the discriminator trained in the Readout 012 Discriminator Training experiment (3 state readout).

  2. Determining the \(\pi_{12}\)-amplitude (x180_ef_amplitude) by fitting a 2D-cosine function to the experimental trace (amplitude versus [ Number of Pi pulses, x180_ef_amplitude ])

image

  1. Sarah Sheldon, Lev S. Bishop, Easwar Magesan, Stefan Filipp, Jerry M. Chow, and Jay M. Gambetta. Characterizing errors on qubit operations via iterative randomized benchmarking. Phys. Rev. A, 93:012301, Jan 2016. doi:10.1103/PhysRevA.93.012301. ↩

  2. Haggai Landa, Dekel Meirom, Naoki Kanazawa, Mattias Fitzpatrick, and Christopher J. Wood. Experimental bayesian estimation of quantum state preparation, measurement, and gate errors in multiqubit devices. Phys. Rev. Res., 4:013199, Mar 2022. doi:10.1103/PhysRevResearch.4.013199. ↩