Skip to content

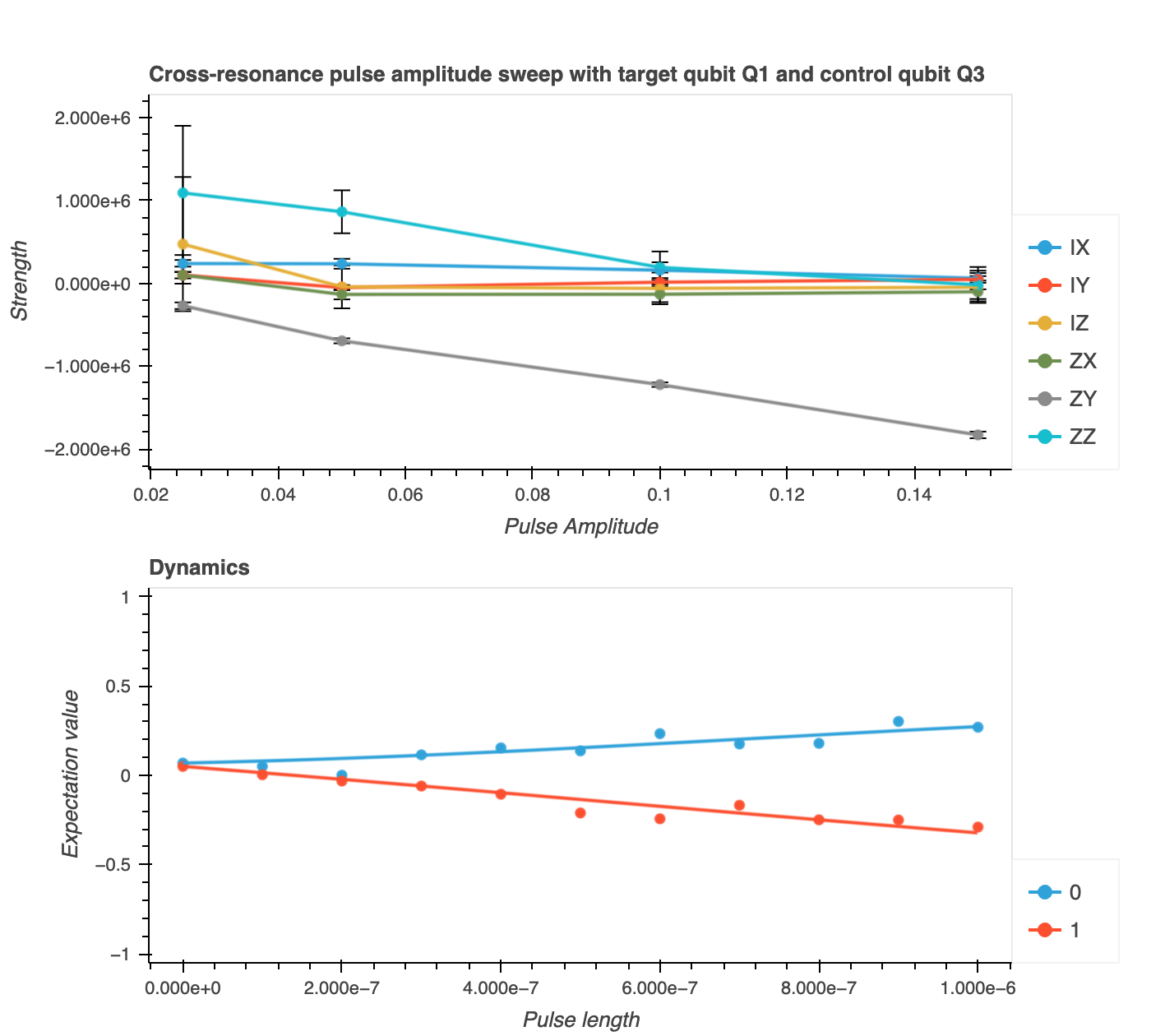
Cross resonance amplitude sweep

The notebook implements cross resonance by sweeping the control pulse amplitude and pulse duration

Description

In cQED, with a multi-qubit architecture, two-qubit entangling operations can be realized using microwave-activated cross-resonance interaction1. This interaction is enabled by the application of a cross-resonant drive tone, corresponding to a qubit drive resonant with a neighboring qubit's transition.

In the laboratory frame2, the Hamiltonian for the two-qubit system can be expressed as

\[H= \omega_{1} \hat{ZI} + \omega_{2} \hat{IZ} + g \hat{XX}.\]

Here, the first two terms describe the qubit Hamiltonians, while the last term represents the qubit-qubit coupling Hamiltonian. We can introduce a drive on the first qubit (referred to as the control qubit \(Q_{C}\)) at the transition frequency \(\Omega_{12}\) of the second qubit (referred to as the target qubit \(Q_{T}\)). In this scenario, considering the frame where both qubits rotate with the drive and under the condition \(g,\Omega_{12} \ll \Delta \omega_{12}\) (where \(\Delta \omega_{12} = \omega_{1} - \omega_{2}\)), the Hamiltonian \(H\) takes the following form:

\[ \begin{aligned} 2\tilde{H}&=\Omega_{ZX} \hat{ZX} + \Omega_{ZY} \hat{ZY} + \Omega_{IX}\hat{IX} + \Omega_{IY} \hat{IY} \\ &+ \Delta \omega_{12} \hat{ZI} + \Omega_{XI} \hat{XI} + \Omega_{YI} \hat{YI} + \varepsilon \hat{ZZ} \end{aligned} \]

where \(\{ \hat{ZX} = \sigma^{z}_{1} \otimes \sigma^{x}_{2}\),...} , and \(\epsilon\) is the cross-Kerr interaction term.

  • The off-resonant control qubit drive terms are defined as \(\Omega_{XI} = \Omega_{12} \cos(\theta_{12})\) and \(\Omega_{YI} = \Omega_{12} \sin(\theta_{12})\). They can be neglected when the drive amplitude \(\Omega_{12} \ll \Delta \omega_{12}\).

  • The cross-resonance interaction terms for the two-qubit system, \(\Omega_{ZX} = \mu \Omega_{12} \cos(\theta_{12})\) and \(\Omega_{ZY} = \mu \Omega_{12} \\ \sin(\theta_{12})\), are similarly dependent on the cross-resonance drive amplitude and phase but also the cross-resonance drive factor \(\mu\).

  • The rotations on the target qubit, \(\Omega_{IX} = \Omega_{12} \nu \cos(\theta_{12}) + \Omega_{12} m_{12} \cos(\theta_{12} + \phi)\) and \(\Omega_{IY} = \Omega_{12} \nu \sin(\theta_{12}) + \Omega_{12} m_{12} \sin(\theta_{12} + \phi)\), are given by the sum of the contribution from the quantum crosstalk characterized by the factor \(\nu\) and the classical crosstalk characterized by the factor \(m_{12}\) and relative phase \(\theta_{12}\).

  • See Ref 2 for further descriptions and definitions of the parameters mentioned here.

Using the results presented in Ref 2, we get the following effective Hamiltonian:

\[2\tilde{H} \approx \Omega^{T}_{CR} \hat{ZX} + \epsilon \hat{ZZ} ,\]

where \(\Omega^{T}_{CR}\) is a selected target rate at which to drive the cross-resonance interaction \(\hat{ZX}\).

From the previous descriptions, it is straightforward to see that the local drive on the control qubit (\(Q_{C}\)), resonant with the first transition frequency of the target qubit (\(Q_{T}\)), introduces an interaction between them. This interaction rate is proportional to the amplitude of the cross-resonant drive, \(\Omega_{12}\).

Experimental steps

  1. Defining the circuits needed to perform cross-resonance tomography, the method _build_single_qubit_ins-\ tructions inside the class CrossResonanceTomography receives qubit characterization and constructs a dictionary containing three key-value pairs:

    1. ctrl_rx180p: It creates a gate instruction named rx180p for the control qubit. The frequency is set to the value obtained from the characterization.

    2. target_rx90p: It creates a gate instruction named rx90p for the target qubit. The frequency is set to the value obtained from the characterization, and the xy_angle is set to 0.

    3. target_ry90m: It creates a gate instruction named ry90m for the target qubit. The frequency is set to the value obtained from the characterization, and the xy_angle is set to -np.pi / 2.

  2. For each pair of the control qubit states (0-1 states) and expectation values in the \(\sigma_x\), \(\sigma_y\), and \(\sigma_z\) bases, denoted as (ctrl_state, exp_val), we perform a CrossResonanceAmplitudeSweep. This process entails applying CrossResonanceTomography while sweeping through pulse_amplitudes and pulse_lengths:

    1. If ctrl_state == 1, append ctrl_rx180p.

    2. Applying a cr_pulse (\(\hat{ZX}\)):

      • If we set echo=True, cr_pulse consists of an echo-gate scheme (to reduce errors in the calibration, a cancellation tone can be applied3. A \(\hat{ZX}\) gate can be formed with two rx180 gates on the control qubit.

      • If we set echo=False, cr_pulse consists of a ctrl_rx180p pulse.

    3. Measuring the resonator transmission and collect the \(I\) and \(Q\) signals:

      • Applying target_ry90m to measure the qubit in the \(\sigma_x\)-basis.

      • Applying target_rx90p to measure the qubit in the \(\sigma_y\)-basis.

      • No extra pulse is applied to measure the qubit in the \(\sigma_z\)-basis.

Analysis steps

  1. Computing the resonator's amplitude (amplitude) signal as a function of pulse_amplitudes and pulse_len-\ gths. Here, we predict the qubit state from the \(IQ\) data by applying the composite_discriminator obtained in the Correlated Readout Error experiment.

  2. Computing the expectation_values (omega_x, omega_y, omega_z) in the (\(\sigma_x\), \(\sigma_y\), \(\sigma_z\)) basis using the populations obtained in step 1.

  3. Computing the off-resonant control qubit drive terms, cross-resonance interaction terms, and rotations on the target qubit (hamiltonian_param) as functions of pulse_amplitudes, i.e., ["IX", "IY", "IZ", "ZX", "ZY", "ZZ"]. We utilize the fit_cross_resonance_curves function, employing the cr_propagator and propagate_state functions to simulate quantum states based on the input parameters (omega_x, omega_y, omega_z) from 2. On one hand, cr_propagator calculates the propagator for a quantum gate corresponding to the cross-resonance interaction over a small time interval. It constructs a 3x3 matrix generator based on the input angular frequencies (omega_x, omega_y, omega_z) and returns the matrix exponential of the generator matrix multiplied by the time step dt. On the other hand, propagate_state iteratively applies the previous propagator to the initial state at each time point in the list ts (pulse_lengths).

image

  1. Chad Rigetti and Michel Devoret. Fully microwave-tunable universal gates in superconducting qubits with linear couplings and fixed transition frequencies. Phys. Rev. B, 81:134507, Apr 2010. doi:10.1103/PhysRevB.81.134507. ↩

  2. A.D. Patterson, J. Rahamim, T. Tsunoda, P.A. Spring, S. Jebari, K. Ratter, M. Mergenthaler, G. Tancredi, B. Vlastakis, M. Esposito, and P.J. Leek. Calibration of a cross-resonance two-qubit gate between directly coupled transmons. Phys. Rev. Appl., 12:064013, Dec 2019. doi:10.1103/PhysRevApplied.12.064013. ↩↩↩

  3. Sarah Sheldon, Lev S. Bishop, Easwar Magesan, Stefan Filipp, Jerry M. Chow, and Jay M. Gambetta. Characterizing errors on qubit operations via iterative randomized benchmarking. Phys. Rev. A, 93:012301, Jan 2016. doi:10.1103/PhysRevA.93.012301. ↩